はじめに
前回、fbprophetの標準設定で株価を予測する時系列モデルを作成しました。作成した時系列モデルの精度を測るために、R2とRMSEの値を計算した結果は下記のとおりでした。
- R2の値:0.0366
- RMSEの値:307.0447
一般的にR2の値は、最低でも0.6以上の値でないと価値無し=予測ができていない、ことを意味しています。
fbprophetには、時系列モデルを作成する際に複数のパラメータを設定することができます。それらのパラメータを調整することで、株価予測の時系列モデルをどれだけ改善できるかを検証してみました。
調整するパラメータについて
パラメータを調整するにあたり、fbprophetのドキュメントを参考にしました。
●時系列モデル作成時に調整したパラメータ
| パラメータ | デフォルト値 | 最適値の範囲 | 説明 |
| changepoint_prior_scale | 0.05 | 0.001~0.5 | このパラメータが時系列モデルの精度に最も影響を与えるようです。トレンドの柔軟性に影響を与えます。値が小さすぎるとトレンドの変化を読めず、値が大きすぎるとトレンドの変化に過敏に反応してしまいます。 |
| changepoint_range | 0.8 | 0.8~0.95 | 0.8とはトレンドの変化を推定する際に使用するデータは、全データの前から80%分のデータとなります。全データを使用することで過学習となることを防ぐために設定します。 |
| seasonality_prior_scale | 10 | 0.01~10 | このパラメータは指定した季節周期をもとに算出する変動の柔軟性を制御します。値が大きければ季節周期の変動は大きくなり、値が小さければ季節周期の変動は小さくなります。 |
| yearly_seasonality | 10 | ドキュメントに記載は無し | 年周期の季節変動の幅を制御します。このパラメータを大きくすると季節変動の幅が大きくなり、小さくすると季節変動の幅を抑制できます。 |
| weekly_seasonality | 10 | ドキュメントに記載は無し | 週周期の季節変動の幅を制御します。このパラメータを大きくすると季節変動の幅が大きくなり、小さくすると季節変動の幅を抑制できます。 |
| growth | linear | linear, logistic | linearは、線形モデルを作成するときに設定すると精度の高いモデルを作成できます。logisticは、売上受注予測や金融予測などの一般的なビジネスの際に設定すると精度の高いモデルを作成できます。logisticを選択する場合は、予測するデータの上限を設定する必要があります。 |
| seasonality_mode | additive | additive, multiplicative | モデルを作成する際に使用する学習データの季節周期の変動を割合で検討する場合は、乗法モデルmultiplicativeを選択します。※補足あり |
●補足
自転車レンタルを例に解説します。
A月B週の平日平均レンタル人数は1000人、休日平均レンタル人数は800人だったとします。この時、乗法モデルの場合は減りを割合と考えて「20%減」となります。加法モデルの場合は「200人減」となります。C月D週の平日平均レンタル人数が2000人だった場合、休日平均レンタル人数を予測する際、乗法モデルと加法モデルの予測は下記の通りです。
<乗法モデル>
A月B週から休日は平日の「20%減」なので、2000×(1-0.2)=1600、なので休日のレンタル人数は1600人と予測します。
<加法モデル>
A月B週から休日は平日の「200人減」なので、2000-200=1800、なので休日のレンタル人数は1800人と予測します。
この例では、乗法モデルを採用したほうが精度が上がります。
●時系列モデル作成時に追加したパラメータ
月周期、四半期周期を追加しました。
fbprophetに月周期、四半期周期を設定するパラメータはありません。
add_seasonalityで自前の周期性を追加することができます。
下記コードを追加して月周期を自前で設定します。
# 月周期を追加する
m1.add_seasonality(name='monthly', period=30.5, fourier_order=5)# 四半期周期を追加する
m1.add_seasonality(name='quarterly', period=365.25/4, fourier_order=5)periodは、1周期の日数を指定します。
fourier_orderは、フーリエ級数の値を指定します。
フーリエ級数の値が大きいと計算に時間が掛かります。
プログラムの動作概要
作成したプログラムの動作概要について下記に記載しました。
- ライブラリの読み込み(1~45行目)
- 株価の取得と加工(47~68行目)
- データを訓練データと検証データに分割(70~88行目)
- グリッドサーチする探索範囲の設定(90~115行目)
- 時系列モデルを探索範囲の値で定義(122~146行目)
- 定義した時系列モデルを学習(148~149行目)
- 指定日数分の株価を予測(151~177行目)
- 学習済み時系列モデルの性能評価(179~192行目)
- 性能評価の結果と時系列モデル作成時の値を保存(196~210行目)
- 結果をCSVに出力(212~217行目)
設定した探索範囲の値で、5.~9.を繰り返し実施します。
プログラムのコード
作成したプログラムのコードは下記となります。
トヨタ自動車(証券コード:7203)の株価を予測する時系列モデルを作成してみました。
48行目で株価を取得しています。証券コードを変更することで、任意の株価を予測できるようになります。
# 警告を無視する
import warnings
warnings.filterwarnings('ignore')
# DataFrameのライブラリを読み込む
import pandas as pd
import pandas_datareader as web
import numpy as np
import math
# グラフ表示関連のライブラリを読み込む
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import japanize_matplotlib
from matplotlib.dates import date2num
# 日付を扱うためのライブラリを読み込む
from datetime import datetime
# fbprophetのライブラリを読み込む
from fbprophet import Prophet
# R2を計算するためのライブラリを読み込む
from sklearn.metrics import r2_score
# RMSEを計算するためのライブラリを読み込む
from sklearn.metrics import mean_squared_error
# グリッドサーチを行うためのライブラリを読み込む
from sklearn.model_selection import ParameterGrid
# 日本の祝日を取得するためのライブラリを読み込む
import jpholiday
# プログレスバーを表示するためのライブラリを読み込む
from tqdm import tqdm
# 時間を扱うためのライブラリを読み込む
import time
# ログを扱うためのライブラリを読み込む
import logging
logging.getLogger('fbprophet').setLevel(logging.WARNING)
# トヨタ(証券コード:7203)の株価を取得する
df = web.DataReader('7203.JP', data_source='stooq', start='2015-01-01', end='2020-12-31')
# 項目名の日本語化
columns = ['開始値', '最高値', '最安値', '終値', '出来高']
# 項目名を日本語に置き換える
df.columns = columns
# 取得した株価を日付で昇順に変換する
df = df[::-1]
# dfはindexに日付を設定している
# df_1を新規に作成し、日付を列として追加する
df_1 = pd.DataFrame()
df_1['日付'] = df.index.values
# df_1に終値を追加する
df_1['終値'] = df.filter(['終値']).values
# 列名をfbprophetで扱える列名に変換する
df_1.columns = ['ds', 'y']
# 訓練データと検証データを分割する
# 訓練データ:2015-01-05 ~ 2020-11-09
# 検証データ:2020-11-10 ~ 2020-12-30
# 分割日sdayを設定する
split_day = pd.to_datetime('2020-11-10')
end_day = pd.to_datetime('2020-12-30')
# 分割日を起点にtrueとfalseを割り当てる
# train_indexは0~1426行目までTrueで、1427~1462行目までFalseとなり、
# test_indexは0~1426行目までFalseで、1427~1462行目までTrueとなる
train_index = df_1['ds'] < split_day test_index = df_1['ds'] >= split_day
# 訓練データと検証データを作成する
x_train = df_1[train_index]
x_test = df_1[test_index]
# 予測データと検証データをグラフ表示する際に使用する日付を設定する
# 設定する日付は2020-11-10 ~ 2020-12-30となる
dates_test = df_1['ds'][test_index]
# グリッドサーチする探索範囲を辞書型で設定する
params = {'changepoint_prior_scale': [0.4, 0.5, 0.6],
'changepoint_range': [0.8, 0.9, 1.0],
'seasonality_prior_scale': [2.0, 3.0, 4.0],
'yearly_seasonality': [10, 20, 30, 40, 50],
'weekly_seasonality': [10, 20, 30, 40, 50],
'monthly_fourier': [3, 4, 5],
'monthly_prior': [0.5, 1.0, 1.5],
'quarterly_fourier': [3, 4, 5],
'quarterly_prior': [0.5, 1.0, 1.5],
'daily_seasonality': [False]}
# 探索範囲として設定した値をgridにセットする
grid = ParameterGrid(params)
# グリッドサーチの結果を保存するデータフレームを用意する
result = pd.DataFrame(columns=['elapsed_time',
'R2',
'RMSE',
'changepoint_prior_scale',
'changepoint_range',
'seasonality_prior_scale',
'monthly_fourier',
'monthly_prior',
'quarterly_fourier',
'quarterly_prior'])
for p in tqdm(grid):
start = time.time()
# モデルを定義する
m1 = Prophet(growth='logistic',
yearly_seasonality=p['yearly_seasonality'],
weekly_seasonality=p['weekly_seasonality'],
daily_seasonality=p['daily_seasonality'],
changepoint_prior_scale=p['changepoint_prior_scale'],
changepoint_range=p['changepoint_range'],
seasonality_prior_scale=p['seasonality_prior_scale'],
seasonality_mode='multiplicative',)
# 月周期を追加する
m1.add_seasonality(name='monthly',
period=30.5,
fourier_order=p['monthly_fourier'],
prior_scale=p['monthly_prior'])
# 四半期周期を追加する
m1.add_seasonality(name='quarterly',
period=365.25/4,
fourier_order=p['quarterly_fourier'],
prior_scale=p['quarterly_prior'])
# cap,floorを設定する
x_train['cap'] = 8500
x_train['floor'] = 0
# モデルを学習する
m1.fit(x_train)
# 予測データを作成する
# 予測する期間は、2020-11-10から2020-12-30の51日分
# futureはデータフレーム形式で、日付データのみが入っている
future_1 = m1.make_future_dataframe(periods=51, freq='D')
# future_1には、株取引が行われてない週末の日付も含まれているので、土日を除外する
# weekdayを使用することで、月~日を0~6の数値として扱うことができる
# 土曜日=5、日曜日=6をfuture_1から除外する
future_no_weekend = future_1[future_1['ds'].dt.weekday < 5]
# futureには、株取引が行われていない祝日の日付も含まれているので、除外する
# jpholidayを含めることで、指定した期間の祝日を取得できる
holidays = jpholiday.between(split_day, end_day)
# 祝日以外の日付を保存するデータフレームを用意しておく
future_no_holidays = future_no_weekend.copy()
# 祝日以外の日付を抽出する
for i, _ in enumerate(holidays):
future_no_holidays = future_no_holidays[future_no_weekend['ds'] != holidays[i][0]]
# cap,floorを設定する
future_no_holidays['cap'] = 8500
future_no_holidays['floor'] = 0
# 予測する
forecast = m1.predict(future_no_holidays)
# forecastから予測部分yhatのみ抽出する
# 2020-11-10から2020-12-30の期間で株取引が行われた日数は36日となる
ypred = forecast[-36:][['yhat']].values
# ytest:予測期間中の正解データを抽出する
ytest = x_test['y'].values
# R2値,RMSEを計算する
score_r2 = r2_score(ytest, ypred)
score_rmse = np.sqrt(mean_squared_error(ytest, ypred))
# R2,RMSEの計算結果を表示する
print(f'R2 score:{score_r2:.4f}')
print(f'RMSE score:{score_rmse:.4f}')
end = time.time() - start
# 結果を保存する
result = result.append({'elapsed_time': round(end, 4),
'R2': score_r2,
'RMSE': score_rmse,
'yearly_seasonality': p['yearly_seasonality'],
'weekly_seasonality': p['weekly_seasonality'],
'daily_seasonality': p['daily_seasonality'],
'changepoint_prior_scale': p['changepoint_prior_scale'],
'changepoint_range': p['changepoint_range'],
'seasonality_prior_scale': p['seasonality_prior_scale'],
'monthly_fourier': p['monthly_fourier'],
'monthly_prior': p['monthly_prior'],
'quarterly_fourier': p['quarterly_fourier'],
'quarterly_prior': p['quarterly_prior']},
ignore_index=True)
# グリッドサーチした結果をCSVに書き込む
now = datetime.now()
f_time = now.strftime('%Y%m%d-%H%M%S')
# 検証結果をcsvに保存する
result.to_csv('./result/result_{}.csv'.format(f_time), index=False, encoding='utf_8_sig')
プログラムコードの要点説明
プログラムコードの要点について説明します。
●グリッドサーチを実行するための準備(30~31行目)
# グリッドサーチを行うためのライブラリを読み込む
from sklearn.model_selection import ParameterGrid- グリッドサーチを行うためにSklearnのParameterGridを使用します。
●グリッドサーチする探索範囲の設定(91~115行目)
# グリッドサーチする探索範囲を辞書型で設定する
params = {'changepoint_prior_scale': [0.4, 0.5, 0.6],
'changepoint_range': [0.8, 0.9, 1.0],
'seasonality_prior_scale': [2.0, 3.0, 4.0],
'yearly_seasonality': [10, 20, 30, 40, 50],
'weekly_seasonality': [10, 20, 30, 40, 50],
'monthly_fourier': [3, 4, 5],
'monthly_prior': [0.5, 1.0, 1.5],
'quarterly_fourier': [3, 4, 5],
'quarterly_prior': [0.5, 1.0, 1.5],
'daily_seasonality': [False]}
# 探索範囲として設定した値をgridにセットする
grid = ParameterGrid(params)
# グリッドサーチの結果を保存するデータフレームを用意する
result = pd.DataFrame(columns=['elapsed_time',
'R2',
'RMSE',
'changepoint_prior_scale',
'changepoint_range',
'seasonality_prior_scale',
'monthly_fourier',
'monthly_prior',
'quarterly_fourier',
'quarterly_prior'])- グリッドサーチする探索範囲を指定します。
探索範囲を指定する際には注意が必要です。上記の探索範囲だと検証する回数は下記となります。
3×3×3×5×5×3×3×3×3=54,675回 - 1回あたりの検証に30秒かかった場合、全ての検証が終えるまでに約455時間かかります。検証する端末のスペックに応じて、探索範囲を絞りながら実施することをお勧めします。
●探索結果の保存(195~209行目)
# 結果を保存する
result = result.append({'elapsed_time': round(end, 4),
'R2': score_r2,
'RMSE': score_rmse,
'yearly_seasonality': p['yearly_seasonality'],
'weekly_seasonality': p['weekly_seasonality'],
'daily_seasonality': p['daily_seasonality'],
'changepoint_prior_scale': p['changepoint_prior_scale'],
'changepoint_range': p['changepoint_range'],
'seasonality_prior_scale': p['seasonality_prior_scale'],
'monthly_fourier': p['monthly_fourier'],
'monthly_prior': p['monthly_prior'],
'quarterly_fourier': p['quarterly_fourier'],
'quarterly_prior': p['quarterly_prior']},
ignore_index=True)- 探索結果をresultに追加(append)します。
●結果をCSVに出力(212~217行目)
# グリッドサーチした結果をCSVに書き込む
now = datetime.now()
f_time = now.strftime('%Y%m%d-%H%M%S')
# 検証結果をcsvに保存する
result.to_csv('./result/result_{}.csv'.format(f_time), index=False, encoding='utf_8_sig')- 探索結果とモデル性能評価結果は、resultフォルダにresult_’%Y%m%d-%H%M%S’.csvのファイル名で保存します。
プログラムの実行結果
プログラムが正常に実行されると、探索結果とモデル性能評価の結果をCSV形式で取得できます。

探索結果からR2とRMSEの値は下記のように改善しました。
| パラメータ調整前 | パラメータ調整後 | 補足 | |
| R2の値 | 0.0366 | 0.56846 | R2の値は1.0に近いほど精度が高いことを意味します。 |
| RMSEの値 | 307.0447 | 205.5012 | RMSEの値は0に近いほど精度が高いことを意味します。 |
各パラメータの最適値は下記の通りです。
これらの値は、2015年~2020年のトヨタ株価を基に算出した値です。他の株価に適合するかは未確認です。他の株価における各パラメータの最適値は、再度検証が必要です。
| パラメータ | 探索範囲 | 最適値 |
| changepoint_prior_scale | 0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0,1.5,2.0 | 0.6 |
| changepoint_range | 0.8,0.9,1.0 | 1.0 |
| seasonality_prior_scale | 0.1,0.5,1.0,1.5,2.0,2.5,3.0,3.5,4.0,4.5 | 4.5 |
| monthly_fourier | 3,4,5,6 | 5 |
| monthly_prior | 0.5,1.0,1.5,2.0 | 1.5 |
| quarterly_fourier | 3,4,5,6 | 3 |
| quarterly_prior | 0.5,1.0,1.5,2.0 | 0.5 |
| weekly_seasonality | 10,20,30,40,50,60 | 20 |
| yearly_seasonality | 10,20,30,40,50,60 | 40 |
まとめ
各パラメータの最適値で時系列モデルを作成し、実データと予測結果を比較してみました。
実データは2020年11月10日~2020年12月30日までとなります。
青色の線が予測した結果です。
前回の予測より改善はしていますが、株購入の参考値としては、まだまだ精度不足です。
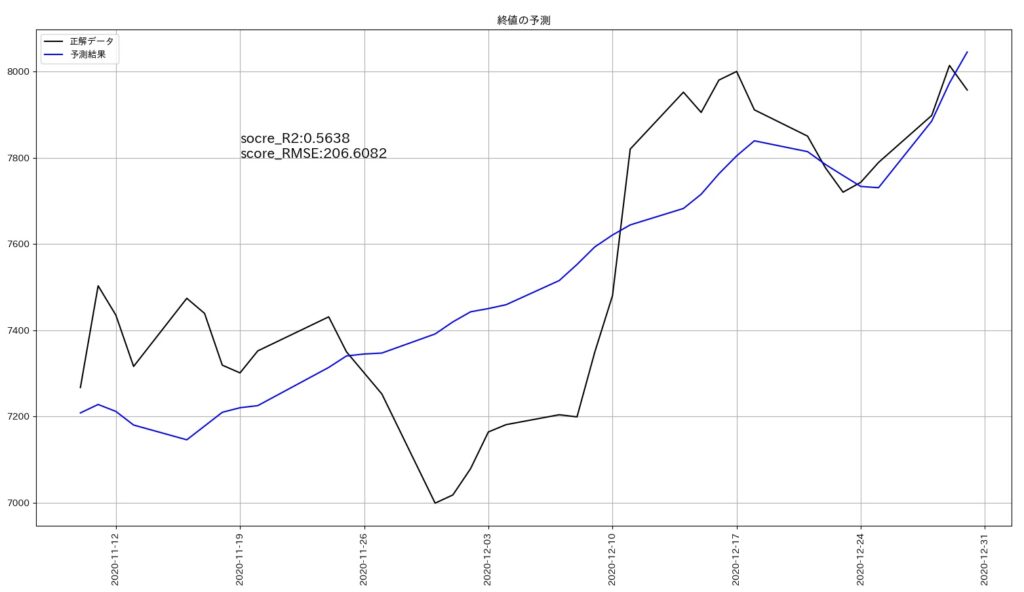
ただ、各パラメータを調整することで、予測精度は上がっています。
fbprophetの扱いは、LSTMより容易でした。またLSTMの株価予測よりR2とRMSEの値は良い結果を出すことができました。まだまだ改善できそうな箇所はあるので、引き続き使い方を学びます。
今後検証について
次回は、「複数の要素を用いた時系列モデル作成と予測」を検証してみます。
パラメータ調整と複数の要素を用いた時系列モデルを作成し、より精度の高い時系列モデルの作成に挑戦してみます。
機械学習とは異なりますが「学習データを読み込んでモデルを作成するWebアプリ」を作成してみたくなりました。誰でも学習データさえ用意すればモデル(AI)を作成でき予測できる、そんなWebアプリを作れないか検討してみます。


コメント