はじめに
前回、KerasのLSTMを使用して株価予測のモデルを作成してみました。モデルを作成する際に使用した変数は、終値(Close)の1つ。取得した株価データには、開始値(Open)、高値(High)、低値(Low)、取引高(Volume)が含まれています。これらのデータを複数使用することで、より精度の高いモデルを作成できないか。より複雑な状況にも対応できるモデルを作成できないか。
複数の変数を用いた予測モデルを作成してみました。
プログラムの説明
前回作成したプログラムとの差分は、太字にしています。
- 取得する株価情報はトヨタ(証券コード7203)
- 取得する期間は2020年1月1日から2020年12月31日(2020年の取引が行われた日は242日)
- 学習に使用する株価データは、開始値(Open)、高値(High)、低値(Low)、取引高(Volume)から選択する
- 学習に使用する株価データが同じ場合、評価値が同一値となるように、乱数シードを固定
- 予測モデルを構築するためのライブラリは、KerasのLSTM
- 予測モデルの学習フローは、1日目から60日目の終値を読み込んで、61日目の終値を予測する
- 予測モデルの層は、2層
- 予測モデルの学習で使用する最適化関数は、adam
- 予測モデルの学習で使用する損失関数は、最小2乗誤差
- 予測モデルの精度評価方法は、決定係数と平均二乗誤差の平方根(RMSE)の2つ
- 予測モデルの精度評価方法で使用する関数は、scikit-learnのr2_scoreとmean_squared_error
プログラムの動作概要
前回作成したプログラムとの差分は、太字にしています。
- ライブラリの読み込み
- 株価を取得する
- 乱数シードを作成する
- 取得した株価から必要なデータを抽出する
- 抽出したデータを正規化する
- 正規化した株価を訓練データと検証データに分割する
- 訓練データを学習用途に整形する
- 予測モデルを定義する
- 定義した予測モデルをコンパイルする
- 検証データでコンパイルした予測モデルの検証を行う
- 検証した結果を評価する
- 予測結果と評価結果を表示する
コード
# 警告を無視する
import warnings
warnings.filterwarnings('ignore')
# ライブラリを読み込む
import math
import pandas_datareader as web
import pandas as pd
import numpy as np
import random
import datetime
# tensorflowのライブラリを読み込む
import tensorflow as tf
# 乱数シードを固定する
tf.random.set_seed(1234)
# kerasのライブラリを読み込む
from keras.models import Sequential
from keras.layers import Dense, LSTM
# scikit-learnの正規を行うライブラリを読み込む
from sklearn.preprocessing import MinMaxScaler
# scikit-learnで決定係数とRMSEの計算を行うライブラリを読み込む
from sklearn.metrics import r2_score, mean_squared_error
# グラフ表示のライブラリとグラフ表示で日本語を表示するためのライブラリを読み込む
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import japanize_matplotlib
from matplotlib import dates as mdates
# トヨタ(証券コード:7203)の株価を取得する
df = web.DataReader('7203.JP', data_source='stooq', start='2020-01-01', end='2020-12-31')
# 取得した株価を日付で昇順に変換する
df = df[::-1]
# csvファイルとして保存する
df.to_csv('toyota_7203.csv', sep=',')
# csvファイルを読み込む
df = pd.read_csv('toyota_7203.csv', sep=',')
# 取得した株価データから予測に使用する列を抽出する
# data = df.filter(['Open', 'High', 'Low', 'Close', 'Volume'])
# data = df.filter(['Open', 'High', 'Close'])
data = df.filter(['Open', 'High', 'Close', 'Volume'])
# 日付を抽出する
data_days = df.iloc[:, 0]
data_days = [datetime.datetime.strptime(s, '%Y-%m-%d') for s in data_days]
# 開始値を抽出する
data_open = df.iloc[:, 1]
# 抽出した株価データをdatasetに代入する
dataset = data.values
# 取得した株価データの8割を訓練データとする
# math.ceil : 小数点以下を切り上げ
# training_data_lenは194となる
training_data_len = math.ceil(len(dataset) * .8)
# 最小値:5839->0、最大値:8014->1となるように正規化する
scaler = MinMaxScaler(feature_range=(0, 1))
scaled_data = scaler.fit_transform(dataset)
# 正規化したデータから訓練で使用する行数分のデータを抽出する
# 0番から193番までが訓練で使用するデータとなる
train_data = scaled_data[0:training_data_len, :]
# 訓練データと正解データを保存する配列を用意する
# x_train:訓練データ
# y_train:正解データ
x_train = []
y_train = []
# 訓練データとして60日分のデータをx_train[]に追加する
# 正解データとして61日目のデータをy_train[]に追加する
for i in range(60, len(train_data)):
xset = []
for j in range(train_data.shape[1]):
a = train_data[i - 60:i, j]
xset.append(a)
x_train.append(xset)
y_train.append(train_data[i, 0])
# 訓練データと教師データをNumpy配列に変換する
x_train, y_train = np.array(x_train), np.array(y_train)
# 訓練データのNumpy配列について、奥行を訓練データの数、行を60日分のデータ、列を抽出した株価データの種類数、の3次元に変換する
x_train_3D = np.reshape(x_train, (x_train.shape[0], x_train.shape[1], x_train.shape[2]))
# LSTMモデルを定義する
n_hidden = 60 # 隠れ層の数
units1 = 25 # 第1層の出力数
units2 = 1 # 第2層の出力数
model = Sequential()
model.add(LSTM(n_hidden, activation='tanh', return_sequences=True, input_shape=(x_train_3D.shape[1], 60)))
model.add(LSTM(n_hidden, return_sequences=False))
model.add(Dense(units1))
model.add(Dense(units2))
# 定義したLSTMモデルをコンパイルする
# 最適化手法:adam
# 損失関数:最小2乗誤差
model.compile(optimizer='adam', loss='mean_squared_error')
# コンパイルしたモデルの学習を行う
batch_size = 1 # バッチサイズ
epochs = 10 # 訓練の回数
model.fit(x_train_3D, y_train, batch_size=batch_size, epochs=epochs)
# 検証データを用意する
# 194番から241番までをテストデータとする
# 最初の194番をテストするためには、134番~193番の終値の株価データが必要となる
# 検証データの最初の番は、訓練データの最後から60を引いた134番となる
# 検証データの総番数は108となる
test_data = scaled_data[training_data_len - 60:, :]
# x_test:検証データ
# y_test:正解データ
x_test = []
y_test = []
# y_test = scaled_data[training_data_len:, :]
# 検証データをセットする
for i in range(60, len(test_data)):
xset = []
for j in range(test_data.shape[1]):
a = test_data[i - 60:i, j]
xset.append(a)
x_test.append(xset)
y_test.append(test_data[i, 0])
# 検証データをNumpy配列に変換する
x_test = np.array(x_test)
# 検証データのNumpy配列について、奥行を訓練データの数、行を60日分のデータ、列を抽出した株価データの種類数、の3次元に変換する
x_test = np.reshape(x_test, (x_test.shape[0], x_test.shape[1], x_test.shape[2]))
# モデルに検証データを代入して予測を行う
predictions = model.predict(x_test)
# モデルの精度を評価する
# 決定係数とRMSEを計算する
# 決定係数は1.0に、RMSEは0.0に近いほど、モデルの精度は高い
r2_score = r2_score(y_test, predictions)
rmse = np.sqrt(mean_squared_error(y_test, predictions))
print(f'r2_score: {r2_score:.4f}')
print(f'rmse: {rmse:.4f}')
# 作業用のnumpy配列を用意する
temp_column = np.zeros(dataset.shape[1] - 1)
# 正規化する前にdatasetと同じnumpy形式に変換する
def padding_array(val):
xset = []
for x in val:
a = np.insert(temp_column, 0, x)
xset.append(a)
xset = np.array(xset)
return xset
# 予測データは正規化されているので、元の株価に戻す
predictions = scaler.inverse_transform(padding_array(predictions))
# 実際の価格、予測の価格をグラフで表示する
# 訓練期間と検証期間を抽出する
data_days_train = data_days[:training_data_len]
data_days_valid = data_days[training_data_len:]
# グラフを表示する領域をfigとする
fig = plt.figure(figsize=(12, 6))
# グラフ間の余白を設定する
fig.subplots_adjust(wspace=0.6, hspace=0.2)
# GridSpecでfigを縦10、横15に分割する
gs = gridspec.GridSpec(9, 14)
# 分割した領域のどこを使用するかを設定する
# gs[a1:a2, b1:b2]は、縦の開始位置(a1)から終了位置(a2)、横の開始位置(b1)から終了位置(b2)
ax1 = plt.subplot(gs[0:8, 0:8])
ax2 = plt.subplot(gs[0:5, 9:14])
# 1番目のグラフを設定する
ax1.set_title('開始値の履歴と予測結果', fontsize=16)
ax1.set_xlabel('日付', fontsize=12)
ax1.set_ylabel('開始値 円', fontsize=12)
ax1.plot(data_days, data_open)
ax1.plot(data_days_valid, predictions[:, 0])
ax1.legend(['実際の価格', '予測の価格'], loc='lower right')
ax1.grid()
# 1番目のx軸ラベルの表示ルールを設定する
data_0_mdates = mdates.MonthLocator([1, 4, 7, 10])
data_0_mdates_fmt = mdates.DateFormatter('%Y-%m')
ax1.xaxis.set_major_locator(data_0_mdates)
ax1.xaxis.set_major_formatter(data_0_mdates_fmt)
# 2番目のグラフを設定する
ax2.set_title('予測の価格と実際の価格の散布図表示', fontsize=16)
ax2.set_xlabel('予測の価格', fontsize=12)
ax2.set_ylabel('実際の価格', fontsize=12)
ax2.scatter(data_open[training_data_len:], predictions[:, 0], label=f'r2_score: {r2_score:.4f} \n rmse: {rmse:.4f}')
ax2.plot(data_open[training_data_len:], data_open[training_data_len:], 'k-')
ax2.legend()
ax2.grid()
fig.savefig('img.png')
plt.show()検証方法
読み込む株価データ以外のパラメータのバッチサイズや訓練回数、活性関数などは固定する。読み込む株価データの違いによる評価値の変動を検証し、最も評価値が高い株価データの組み合わせを探す。
- 検証1
開始値(Open)と高値(High)、低値(Low)、取引高(Volume)のどれか1つ選択してモデルを作成する。評価値が高い=開始値(Open)と相性の良い変数を特定する。
- 検証2
検証1で特定した変数と、残りの変数から1つ選択してモデルを作成する。評価値が高い変数の組み合わせを特定する。
- 検証3
検証2を繰り返す
検証結果
- 検証1の結果
開始値(Open)と相性が良い変数は、高値(High)となった。検証2では、開始値(Open)と高値(High)を固定して検証する。
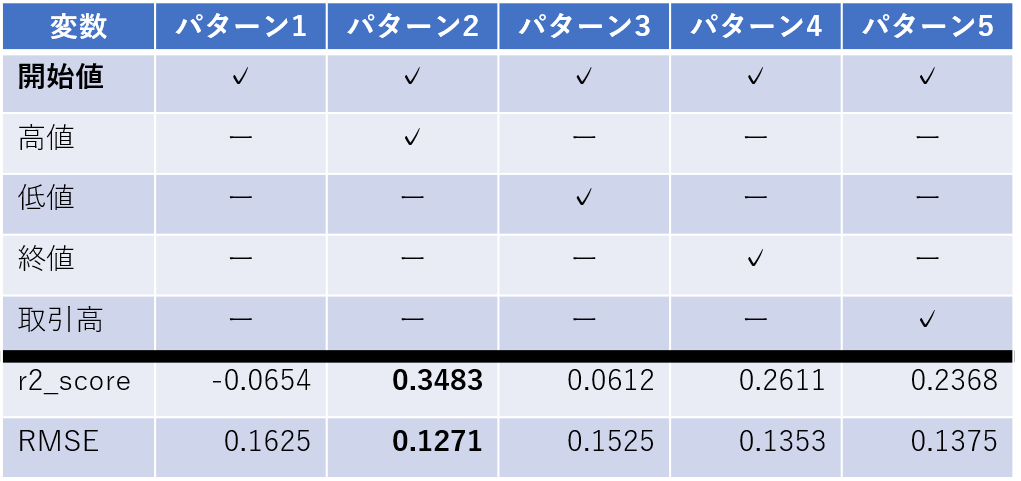
「✓」が入っている変数をモデル学習の際に使用。
- 検証2の結果
開始値(Open)+高値(High)と相性が良い変数は、取引高(Volume)となった。低値(Low)を含めてモデルを作成すると評価値は0.2861となり0.3483より下がった。検証3では、開始値(Open)と高値(High)、取引高(Volume)を固定して検証する。

- 検証3の結果
開始値(Open)+高値(High)+取引高(Volume)と相性が良い変数は、終値(Close)となった。ただし、終値(Close)を含めてモデルを作成すると評価値は3.450となり3.853より下がった。

検証のまとめ
検証した結果、開始値を予測するモデルを作成する際、高値と取引高を含めたモデルを作成することで、評価値が高くなることが判りました。
モデルを作成する際、多くの変数を読み込むことで評価値が高いモデルを作成できる、と考えていたのですが、そうでないことを学ぶことができました。
次回、試したいこと。
各パターンを検証した際、その都度コードを編集していました。モデルの精度を上げるためのパラメータを探索する方法にグリッドサーチがあります。グリッドサーチの方法を学び、各パラメータの調整と検証の作業について、作業を軽減できないか試してみます。



コメント